Maintaining Distributed Data Structures in Dynamic Peer-to-Peer Networks

Antonio Cruciani\(^2\)
antonio.cruciani@gssi.it
John Augustine\(^1\)
Iqra A. Gillani\(^3\)
augustine@cse.iitm.ac.in
iqraaltaf@nitsri.ac.in


Peer-to-Peer Networks
A network of peer nodes
mostly decentralized, but some central control
Some real-world examples
Bitcoin, Skype, Bit Torrent, Signal, Cloudmark, CrashPlan, Sysform, etc....
Prevailing Definition
- The network is highly dynamic
- The network experiences heavy churn
(up to 50% new nodes every hour)
- Overlay edges are created and destroyed all the time
Key Challenges
Peer-to-Peer Networks: architecture
Underlying Internet (Complete Connectivity)
Overlay network
can be structured or unstructured
Dynamic Networks with Churn (DNC) Model
Synchronous.
All nodes follow the same clock. In each round \(r=1,2,\dots\)
- Each node sends/receives \(polylog(n)\) messages per round
- Message size \(polylog(n)\)
- Nodes perform local computations
Adversarial Dynamism.
An oblivious adversary (knows algorithm, but not the coin toss outcomes) designs churn
\(\mathcal{G} = (G^0,G^1,\dots G^r,\dots)\)
DNC Model: setting
Churn.
Stable Network Size.
Up to \(\mathcal{O}(n/\log n)\) nodes leave/join the network per round.
Number of nodes \(n\) unchanged over time
(In each round: # churned out = #churned in)
Can be relaxed!
Connectivity assumption.
The adversary cannot connect all the new nodes to only one peer in the network
DNC Model: setting
- Every node can send up to \(\mathcal{O}(polylog(n))\) messages
- Each message of size \(\mathcal{O}(polylog(n))\)
Node Capacitated Network.
Connectivity assumption.
The adversary cannot connect all the new nodes to only one peer in the network
Recap
\(\mathcal{O}(\log n)\) rounds bootstrap phase
churn rate of up to \(\mathcal{O}(n/\log n)\) per round
Adverary wakes up
Maintenance Phase

Algorithm initialization
We need to cope with the churn
DNC Model: some works
- Expander graph maintenance [Augustine et al. FOCS '15]
- Agreement [Augustine et al. PODC '13]
- Overlay Construction [Götte et al. PODC 2021]
- Information Spreading [Augustine et al. DISC 2016]
.
.
.
What about maintaining a distributed data structure?
Our Problem
- Build and maintain a data structure despite the churn
- Data structure must be queryable at each round
Is \(x\) in the DS ?
round \(r\)
Yes
No
If life of the element subsumes \([r,r+Q]\)
If no node \(x\) with effective life-time overlapping \([r,r+Q]\)
DS
\(Q\)
- Each node in the overlay has one element in the DS
Dynamic Resource Competitiveness
Our distributed algorithm must be efficient
Workload: #Created Edges + #Messages
\(t_{start}-\alpha\)
\(\alpha = \mathcal{O}(\log n)\)
\(\beta = polylog(n)\)
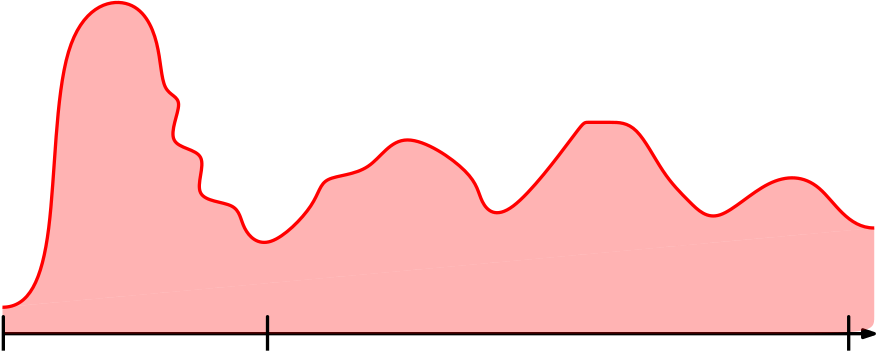
Churn
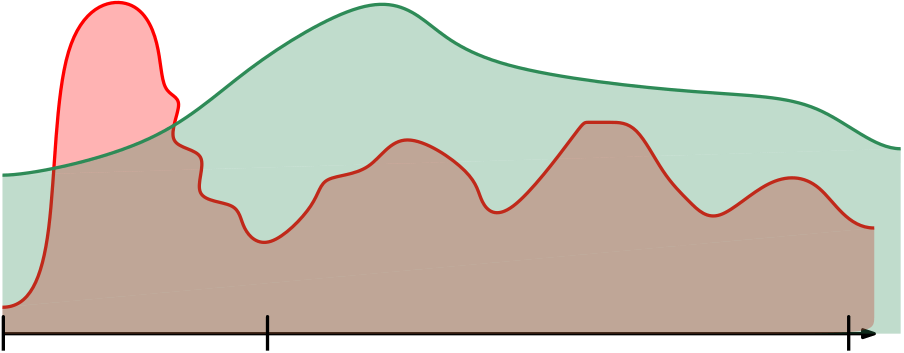
Workload \(\leq\beta\cdot\)Churn(\(t_{start}-\alpha,t_{end}\))
\(t_{start}\)
\(t_{end}\)
Dynamic Resource Competitiveness
Our distributed algorithm must be efficient
Workload: #Created Edges + #Messages
Algorithm is \((\alpha,\beta)\)-dynamic resource competitive if
for any time instants \(t_{start}<t_{end}\)
\(\text{Workload}(t_{start},t_{end}) = \mathcal{O}(\beta\text{Churn}(t_{start}-\alpha,t_{end}))\)
Definition:
In our case:
\(\alpha = \mathcal{O}(\log n)\)
\(\beta = polylog(n)\)
Skip List

H
H
T
\(-\infty\)
\(\infty\)
\(22\)
\(56\)
\(78\)
\(79\)
\(83\)
\(97\)
Tail
Head
LV. 0
LV. 1
LV. 2
Is \(83\) in the SL. ?
Our Idea
Let's decouple the
data structure
from the overlay network
Spartan: The Overlay Network
0
1
0
0
1
2
3
Level
Row
Committee
Committee:
- Clique of \(\Theta(\log n)\) random nodes
- Nodes randomly change committee
- Cannot be destroyed w.h.p
Augustine et. al [J.P.D.C. 2021]
Dealing with the nodes removed by the adversary
Gets removed
Gets replaced by committee
''Virtual node''
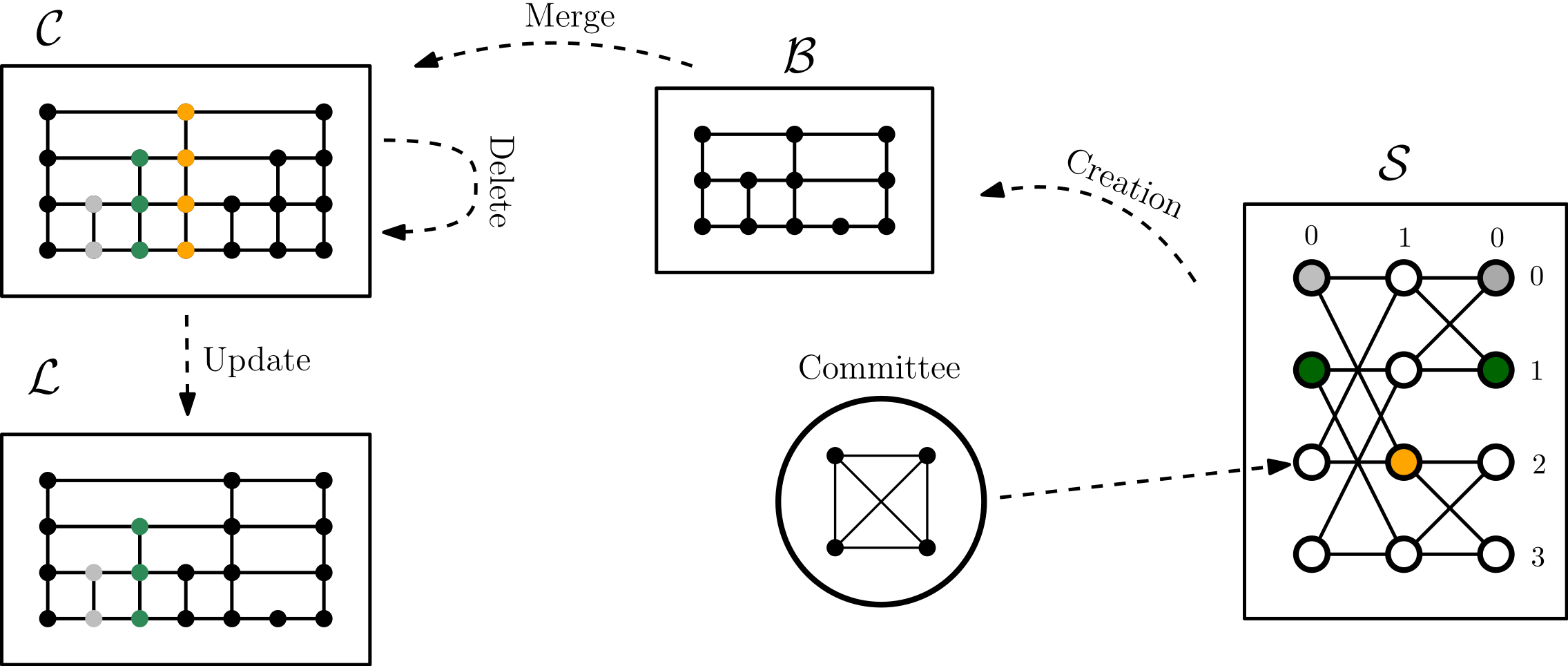
The Maintenance Cycle
1
2
3
4

Overlay Network
Clean Network
Buffer Network
Live Network
The Architecture

Clean Network
Buffer Network
Spartan Network
Live Network
Deletion Phase
\(a\)
\(b\)
\(c\)
\(d\)
\(e\)
\(f\)
\(g\)
\(h\)
\(i\)
\(j\)
\(\infty\)
\(-\infty\)
We can delete all the virtual nodes in \(\mathcal{O}(\log n)\) rounds w.h.p
- Tree Formation
- Propagation
\(\mathcal{O}(\log n)\) w.hp.
\(\mathcal{O}(\log n)\) w.h.p.
\(k\)
\(\ell\)
\(f\)
Deletion Phase
\(a\)
\(b\)
\(c\)
\(d\)
\(e\)
\(f\)
\(g\)
\(h\)
\(i\)
\(\ell\)
\(\infty\)
\(-\infty\)
We can delete all the virtual nodes in \(\mathcal{O}(\log n)\) rounds w.h.p
- Tree Formation
- Propagation
\(\mathcal{O}(\log n)\) w.hp.
\(\mathcal{O}(\log n)\) w.h.p.
Buffer Creation Phase
We need to create a new Buffer Network
1. Create a sorted list of new elements added by the adversary
2. Build a skip list
Can be done in \(\mathcal{O}(\log^3 n)\) [Augustine et al., SPAA 2019 ]
Can we do better?
Buffer Creation Phase
We can create the Buffer in \(\mathcal{O}(\log n)\) rounds!
Ajtai, Komlós, and Szemeréd (AKS) Network [STOC, 1983]
How? Using sorting networks
3
4
2
1
Input
Output
3
4
1
2
1
3
4
2
1
2
3
4
What sorting network?
How can we use it?
Maggs et al. [Algorithmica, 2000]
Can be efficiently simulated on multibutterfly networks!
Buffer Creation:
1. Build a multibutterfly \(\mathcal{M}\)
2. Run AKS on \(\mathcal{M}\)
3. Build the upper level of the skip list
\(\mathcal{O}(\log n)\) w.h.p.
\(\mathcal{O}(\log n)\)
\(\mathcal{O}(\log n)\) w.h.p.
# Of Rounds
Buffer Creation Phase
AKS


Buffer Creation Phase
AKS


Delete algo.
Merge Phase
We need to merge the Buffer Network with the Clean Network
Can be done in \(\mathcal{O}(\log n)\) rounds w.h.p.
\(\mathcal{O}(n)\)


\(\mathcal{O}(n)\)
\(-\infty\)
\(\infty\)
\(5\)
\(13\)
\(27\)
\(45\)
\(50\)
\(ls\)
\(rs\)
\(1\)
\(23\)
\(25\)
\(55\)
\(98\)
\(-\infty\)
\(\infty\)
\(5\)
\(13\)
\(27\)
\(45\)
\(50\)
\(ls\)
\(rs\)
\(1\)
\(23\)
\(25\)
\(55\)
\(98\)
Buffer Network
Clean Network
Merge Phase: WAVE Protocol
\(-\infty\)
\(\infty\)
\(5\)
\(13\)
\(27\)
\(45\)
\(50\)
\(ls\)
\(rs\)
\(1\)
\(23\)
\(25\)
\(55\)
\(98\)
WAVE Protocol: Down the rabbit hole
\(ls\)
\(rs\)
\(1\)
\(23\)
\(25\)
\(55\)
\(98\)
\(23\)
\(25\)
\(25\)
\(55\)
\(25\)
\(1\)
\(98\)
\(55\)
Parent-Children relationship
WAVE Protocol: Down the rabbit hole
Cohesive Group
Group Leader
Followers
WAVE Protocol: Down the rabbit hole
- The leader of a Cohesive Group is in charge of traversing the target skip list
- Every time the leader moves on the Clean Network:
1. Informs its followers
2. Informs its children
- Every time a follower receive a message:
1. Virtually walks on the Clean Network
2. Informs its children
\(ls\)
\(rs\)
\(1\)
\(23\)
\(25\)
\(55\)
\(98\)
\(-\infty\)
\(\infty\)
\(5\)
\(13\)
\(27\)
\(45\)
\(50\)
\(ls\)
\(1\)
\(23\)
\(25\)
\(1\)
\(ls\)
Some Children
Cohesive Group
\(23\)
\(98\)
\(rs\)
\(ls\)
\(ls\)
\(1\)
\(23\)
\(25\)
\(1\)
\(ls\)
\(23\)
\(98\)
\(rs\)
Some Children
Cohesive Group(s)
\(23\)
\(98\)
\(rs\)
\(ls\)
\(-\infty\)
\(\infty\)
\(5\)
\(13\)
\(27\)
\(45\)
\(50\)
\(ls\)
\(23\)
\(98\)
\(rs\)
\(98\)
\(rs\)
\(25\)
\(55\)
\(1\)
Update Phase
- We need to Update the Live Network with the Clean Network
- Two type of edges:
Present in the Clean Network
Present in both Networks
Recap

Main Result
- Can be extended to skip graphs
- Works with multiple keys on each node of the overlay
- Can build and maintain a skip list despite heavy churn
- \(\mathcal{O}(\log n)\) rounds maintenance algorithm
- \((\alpha,\beta)\)-Dynamic Resource Competitive
(\(\alpha = \mathcal{O}(\log n)\) and \(\beta = polylog(n)\))
- The skip list is maintained for \(n^c, (c\geq 1)\) rounds w.h.p.
Future Work
What if there are Byzantine nodes in the network ?
Thank You

Our paper