PROPAGATE: a seed propagation framework to compute Distance-based metrics on Very Large Graphs
Antonio Cruciani\(^1\) Giambattista Amati\(^2\)
Daniele Pasquini\(^3\) Paola Vocca\(^3\)
Simone Angelini\(^2\)



\(^1\)
\(^2\)
\(^3\)
Setup
- We have a very large graph (social, web)
- We want to understand something about its global structure (not triangles/degree distribution etc.)
- We consider distance-based metrics (diameter, average distance, etc.)
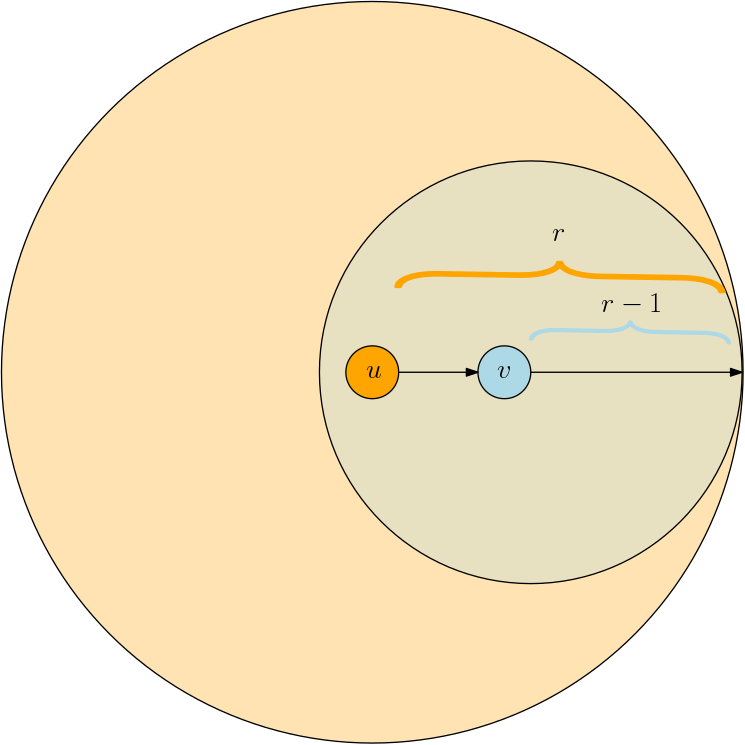
Ball of radius \(r\)
For each node \(u\in V\) the ball of radius \(r\) is
The overall number of reachable pairs at distance \(r\) is
Diameter and Effective Diameter
Diameter
Effective Diameter
\(\tau\in [0,1]\)
In this work we consider \(\tau=0.9\), i.e., the \(90^{th}\) percentile distance between the nodes
Average Distance and Connectivity Rate
Average Distance
Connectivity Rate
Notice that the more the graph is connected the higher is \(\alpha\), and vice versa
How can we compute distance-based metrics?
Iteratively, by merging the neighborhoods [Palmer et al., (KDD' 02)]
Easy but expensive
- Each set uses linear space; overall quadratic
- Impossible!
- What if we use approximate sets?

- MHSE [Amati et al., (Bigdata' 17)] uses MinHash counters
- HyperANF [Vigna et al., (WWW' 11)] uses HyperLogLog counters
PROPAGATE framework
Given a set of seed nodes \(S = \{x_1,x_2,\dots,x_s\}\)
Each \(u \in V\) has a Boolean signature array \(\texttt{Sig}(u)\) of length \(s\) in which
- Simulate a diffusion process in which these bits spread across the network
- Count the number of newly infected nodes at each round
Idea:
PROPAGATE-P
Running time
Required Space
\(\mathcal{O}(\Delta\cdot m)\)
\(\mathcal{O}(s\cdot n+m)\)
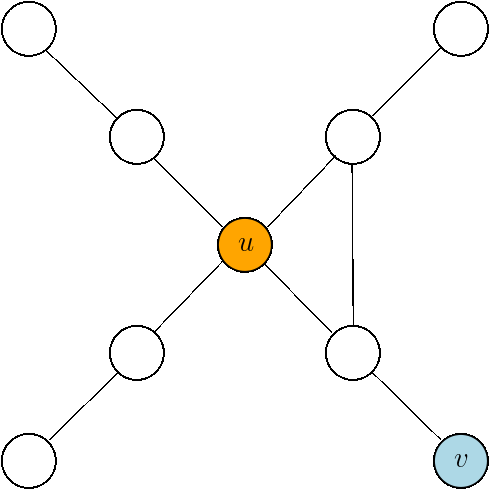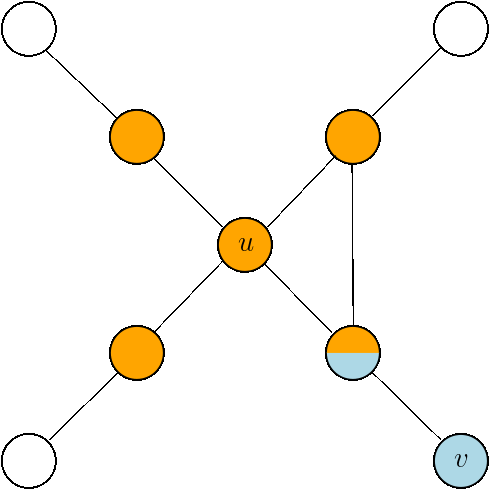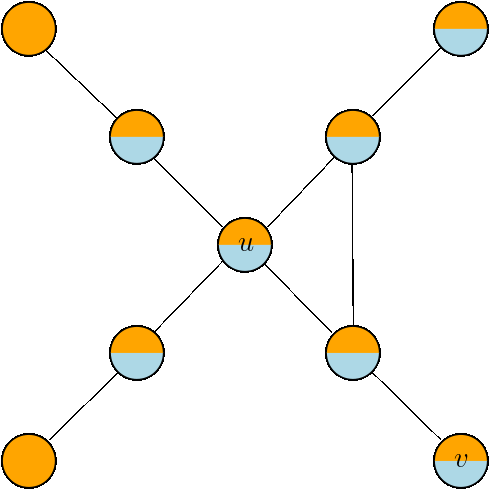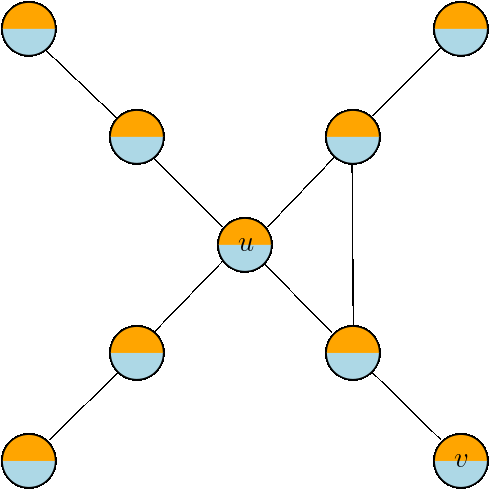
Bit Spreading Process:
for each \(u\in V\):
\(\texttt{Sig}_{\texttt{new}}(u) =\) bitwise OR between \(\texttt{Sig}(u) \) and the neighbors' signature
Count the newly infected nodes:
\(\displaystyle\sum_{u\in V}||\texttt{Sig}(u)\oplus \texttt{Sig}_{\texttt{new}}(u) || \)
PROPAGATE-S
Every node \(u\in V\) has a signature of \(1\) bit
Bit spreading process executed sequentially
Running time
Required Space
\(\mathcal{O}(s\cdot\Delta\cdot m)\)
\(\mathcal{O}( n+m)\)
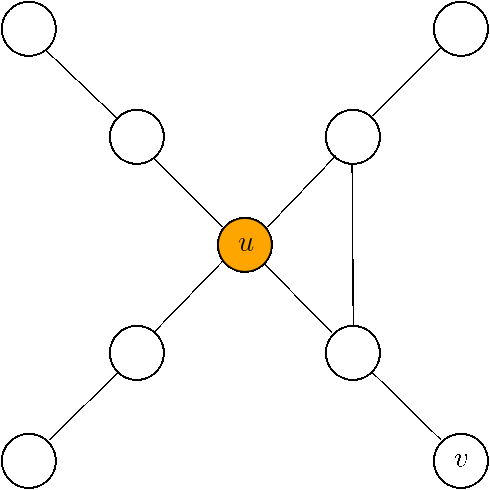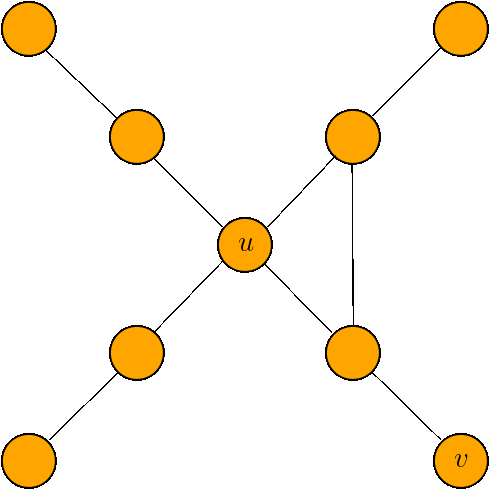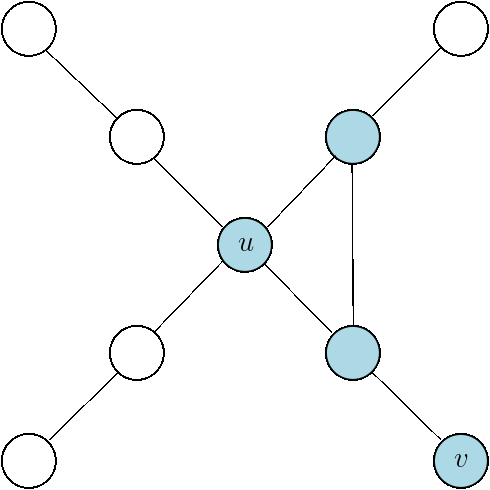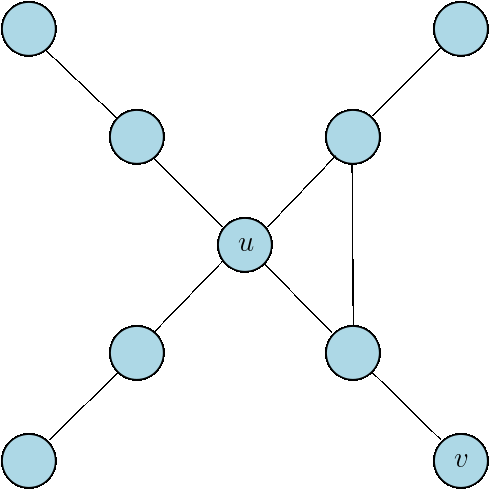
Theoretical guarantees
Theorem
With a sample of \(s=\Theta\left(\frac{\ln n}{\varepsilon^2}\right)\) nodes, with high probability, PROPAGATE framework computes:
- the average distance with the absolute error bounded by \(\varepsilon \frac{\Delta}{\tilde{\alpha}}\)
- the effective diameter with the absolute error bounded by \(\frac{\varepsilon} {\tilde{\alpha}}\)
- the diameter with the absolute error bounded by \(\frac{\varepsilon} {\tilde{\alpha}}\)
- the connectivity rate \(\alpha\) with the absolute error bounded by \(\varepsilon\)
Time
Space
Algorithm
PROPAGATE-P
PROPAGATE-S
\(\mathcal{O}(\frac{\ln n}{\varepsilon^2}\cdot\Delta\cdot m)\)
\(\mathcal{O}(n+m)\)
\(\mathcal{O}(\Delta\cdot m)\)
\(\mathcal{O}(\frac{\ln n}{\varepsilon^2}\cdot n+m)\)
Experimental Setting
We compare our algorithms with
HyperANF
MHSE
RandBFS
Time
Space
\(\mathcal{O}(\Delta\cdot m)\)
\(\mathcal{O}(\Delta\cdot m)\)
\(\mathcal{O}(s\cdot m)\)
\(2\cdot s\cdot n\cdot \log_2(\log_2 (n/s))\) bits
\(\mathcal{O}(n+m)\)
\(2\cdot s\cdot n\cdot \log_2n\) bits
Experimental Setting
Every algorithm is run using 256 seeds/registers
Every algorithm is run 10 times
Machine used: server equipped with AMD Opteron 6376 CPU (2.3GHz), 32 cores and 64 GB of RAM
All the algorithm have been implemented in Java

Graphs

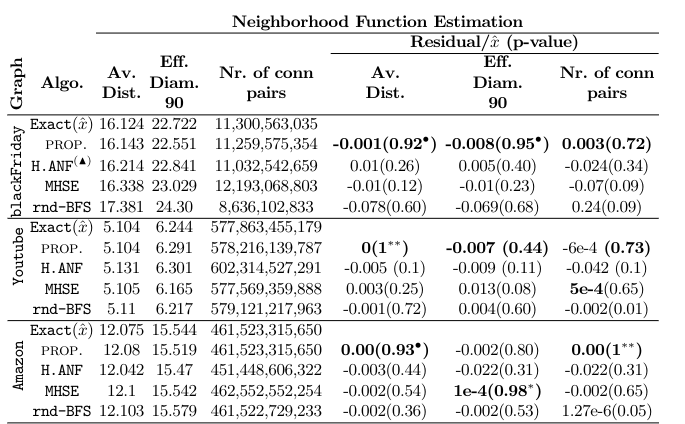
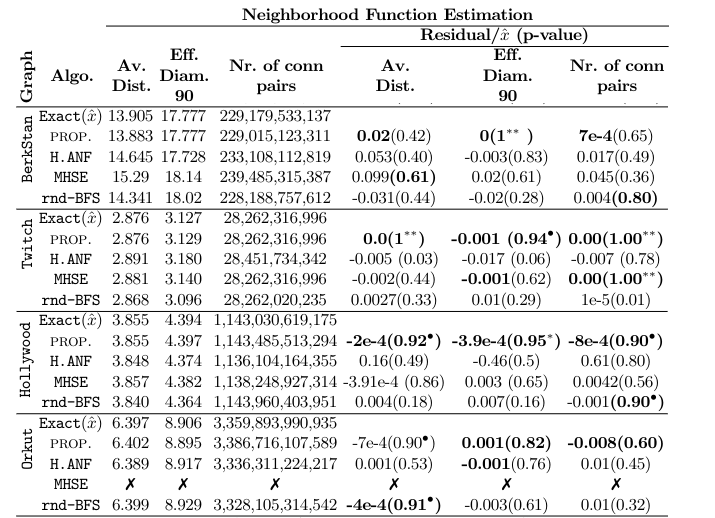
Accuracy and Effectiveness
Speed
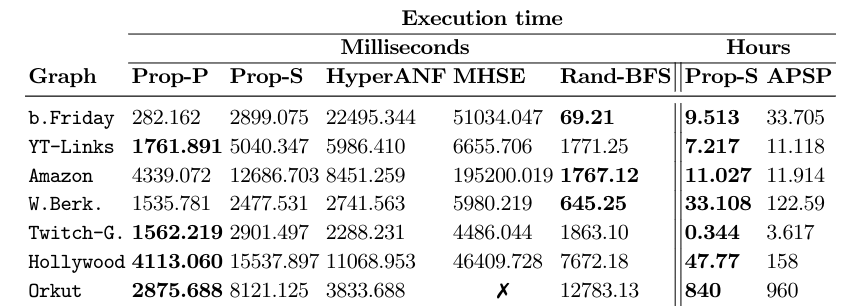
Estimation of distance-based metrics
Ground truths computation
Estimating Distance Metrics on huge graphs

Conclusions
In this work:
Future directions:
- Introduced a novel approach to compute the distance-based metrics
- Theoretically and experimentally showed the advantage of using our framework over the state of the art
- Extend PROPAGATE to compute centrality measures of nodes/edges and to community detection tasks
- Showed that our framework is the only available option to approximate distance-based metrics when we do not have access to servers with a large amount of memory
Thank You

Our graph library
Additional Experiments: PROPAGATE-S' incremental approach
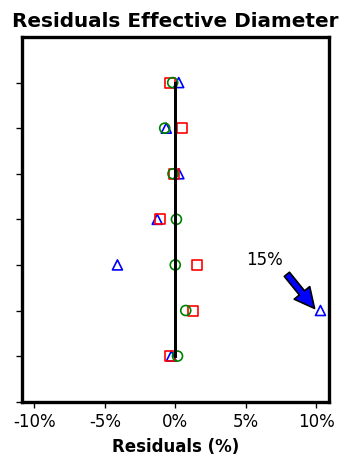
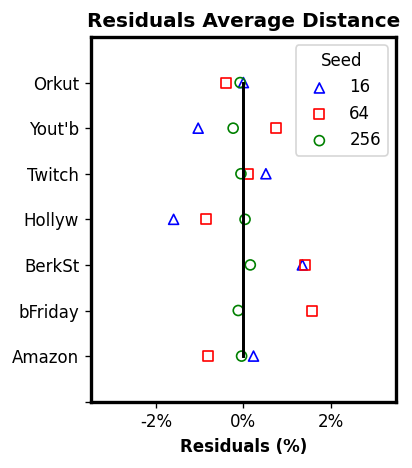
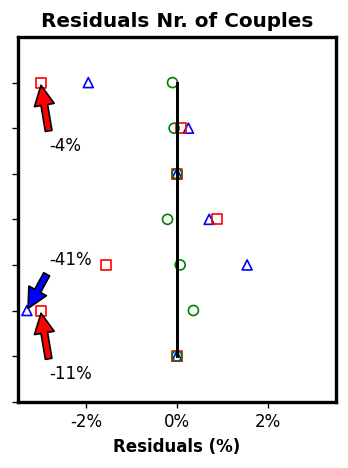
PROPAGATE framework
Given a set of seed nodes \(S = \{x_1,x_2,\dots,x_s\}\)
Each \(u \in V\) has a Boolean signature array \(\texttt{Sig}(u)\) of length \(s\) in which
- Simulate a diffusion process in which these bits spread across the network
- Count the number of newly infected nodes at each round
Idea:

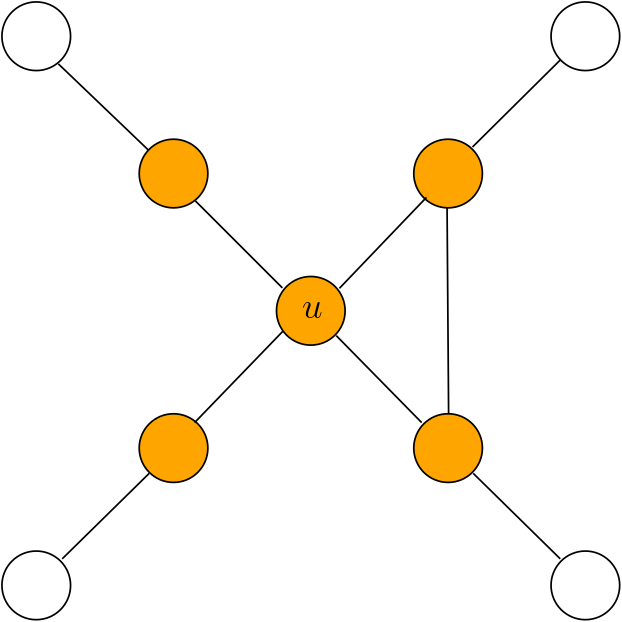
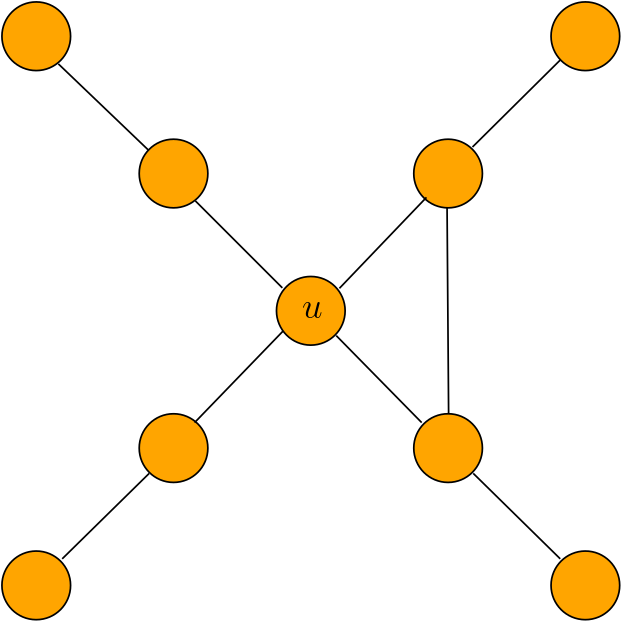
Bit Spreading Process:
for each \(u\in V\):
\(\texttt{Sig}_{\texttt{new}}(u) =\) bitwise OR between \(\texttt{Sig}(u) \) and the neighbors' signature
Count the newly infected nodes:
\(\displaystyle\sum_{u\in V}||\texttt{Sig}(u)\oplus \texttt{Sig}_{\texttt{new}}(u) || \)